La precisión de datos es uno de los elementos claves de la computación. Su importancia es altamente importante en simulaciones científicas hasta el entrenamiento de modelos de lenguaje. Elegir cómo se representa un número afecta directamente en la confiabilidad de los resultados
Un poco de contexto histórico sobre la precisión de datos
Todas las consultas en internet, desde las búsquedas en Google, los procesos de consultas de ChatGPT, y desde luego cuando las supercomputadoras predicen el clima global, detrás de cada proceso hay un cálculo. ¿Cuánta precisión necesitamos realmente para cada proceso?

A medida que evolucionaron las supercomputadoras desde ENIAC, hasta las más modernas como Leftraru en la Universidad de Chile, El Capitán del Laboratorio Nacional Lawrence, Aurora en el Laboratorio Nacional Argonne, los científicos computacionales establecieron gradualmente la doble precisión (FP64) como estándar de oro, formalizado con la norma IEEE 754 de 1985.
La industria de los videojuegos priorizó la velocidad sobre la precisión: era más importante renderizar millones de píxeles por segundo que lograr cálculos matemáticamente perfectos, popularizando FP32.
Entrenar modelos de lenguaje masivos (LLM) como GPT, requiere una cantidad incontable de data, que hasta los PCs más poderosos se saturan, porque a mayor precisión (como FP64), mayor es el consumo de memoria.
Por lo anterior es que técnicas como FP16 y enteros de 8 bits (INT8), que son representaciones numéricas menos precisas, son claves en los procesos de entrenamientos de las IA y, desde luego, hacer viables económicamente nuevos modelos.
El concepto de precisión
Desde el punto de vista técnico, la precisión de datos se refiere al grado de fidelidad con que un formato digital representa un valor del mundo real. Este concepto implica un equilibrio complejo entre cuatro factores clave:
- Eficiencia energética: consumo de energía durante los cálculos
- Fidelidad numérica: qué tan exactamente se puede representar un número
- Velocidad de cálculo: rapidez en el procesamiento de operaciones
- Uso de memoria: cantidad de espacio requerido para almacenar datos
Es importante distinguir precisión de exactitud, ya que ambos conceptos suelen confundirse, pero responden a propiedades distintas.
- Exactitud: indica cuán cercano está un valor obtenido respecto al valor real o verdadero.
- Precisión: evalúa qué tan consistentes o repetibles son varias mediciones bajo las mismas condiciones.
Para entender la idea, veamos el siguiente ejemplo:
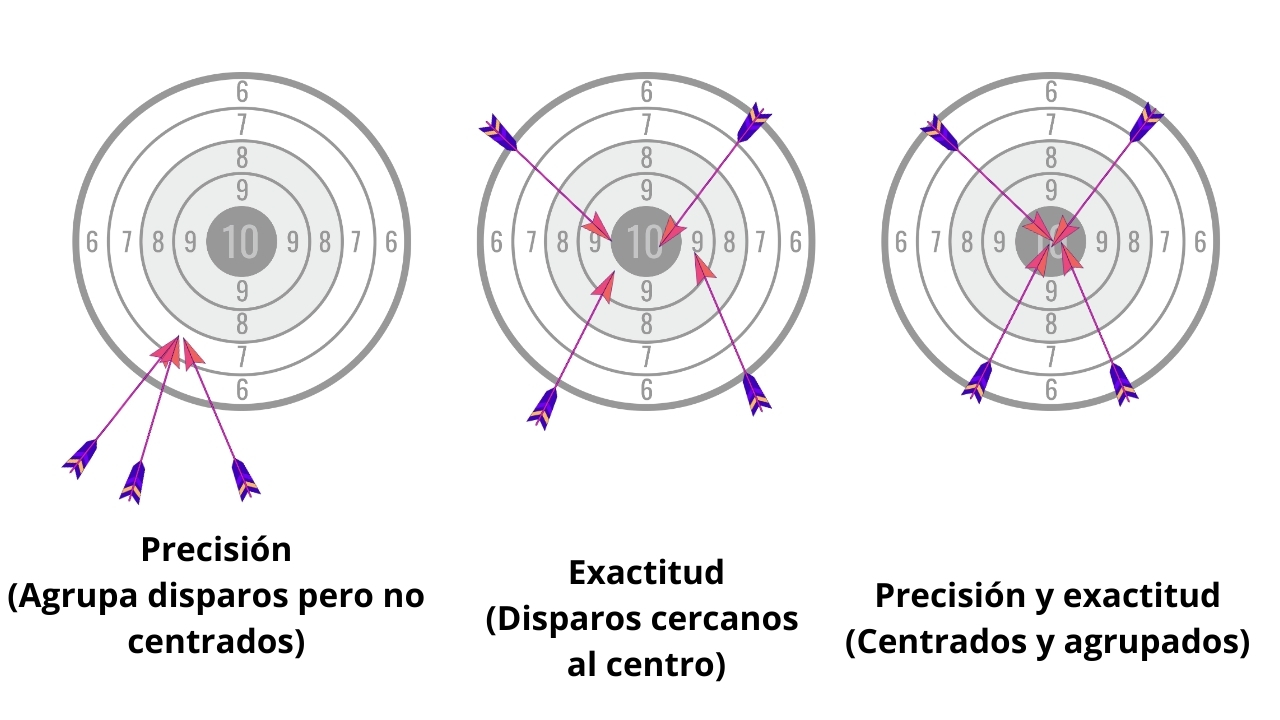
- Un tirador preciso agrupa todos sus disparos en un área reducida, aunque no estén centrados.
- Un tirador exacto distribuye sus disparos cerca del centro, aunque de forma dispersa.
- El objetivo ideal es lograr alta precisión y alta exactitud al mismo tiempo.
Tipos de Datos Numéricos
En general, tendremos dos conjuntos de datos: Los enteros y los de punto flotante.
Los enteros (INT)
Representan números enteros de manera exacta, sin fracciones ni errores de redondeo, siempre que el número esté dentro del rango del tipo de dato. Su única limitación es el rango, determinado por el número de bits que utilizan.
Datos numéricos de punto flotante (FP)
Es un sistema que emula números reales (con fracciones) mediante una aproximación similar a la notación científica.
- Permite representar un rango de valores extremadamente amplio, desde números muy grandes hasta otros prácticamente infinitesimales.
- Todo esto se logra con una cantidad fija de bits, lo que optimiza el almacenamiento.
- La flexibilidad tiene un costo: la mayoría de los números reales no pueden representarse de forma exacta.
- Para resolverlo, los valores deben ser redondeados, lo que introduce pequeños errores acumulativos en los cálculos.
El punto flotante emula los reales, pero solo representa de forma exacta algunos racionales (k/2ⁿ); el resto —incluidos π y √2— se almacena como aproximaciones redondeadas.
El estándar IEEE 754
Para evitar que cada fabricante definiera su propio sistema numérico, el Instituto de Ingenieros Eléctricos y Electrónicos (IEEE) estableció en 1985 el estándar 754. Esta norma define de manera precisa cómo deben representarse y calcularse los números en cualquier computador y dispositivo electrónico.
Componentes principales del IEEE 754:
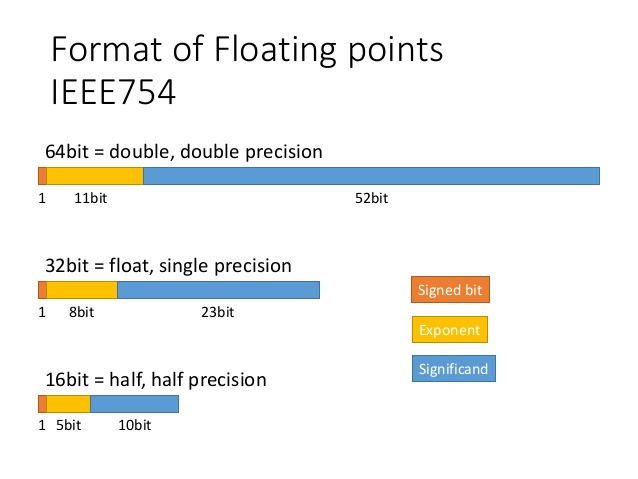
- Formatos de representación: especifica cómo se almacenan los números en distintos tamaños (FP16, FP32, FP64).
- Procedimientos de redondeo: establece reglas uniformes para aproximar valores que no pueden representarse exactamente.
- Manejo de excepciones: define el comportamiento en situaciones especiales, por ejemplo:
- División por cero → resultado: Infinito
- Operaciones indefinidas → resultado: NaN (Not a Number)
- Desbordamientos → resultado según el rango permitido
Esto es clave para que los softwares funcionen de manera consistente y predecible en cualquier hardware moderno.
Uso de la precisión en modelos de IA y HPC
Con el auge de la IA, y de las supercomputadoras que deben procesar volúmenes masivos de información, la precisión numérica ha adquirido una relevancia fundamental. La elección del formato —sea de baja precisión para acelerar el entrenamiento de modelos, o de máxima fidelidad para garantizar la estabilidad en simulaciones científicas— se ha vuelto un factor determinante en el rendimiento, el consumo de recursos y la confiabilidad de los resultados.
Uso en el entrenamiento de inteligencia artificial (IA)
El entrenamiento de redes neuronales, tradicionalmente realizado en FP32 por su estabilidad, se transformó en un cuello de botella debido al alto consumo de memoria. La solución fue el entrenamiento con precisión mixta, que combina la eficiencia de los formatos de 16 bits con la estabilidad numérica de FP32.
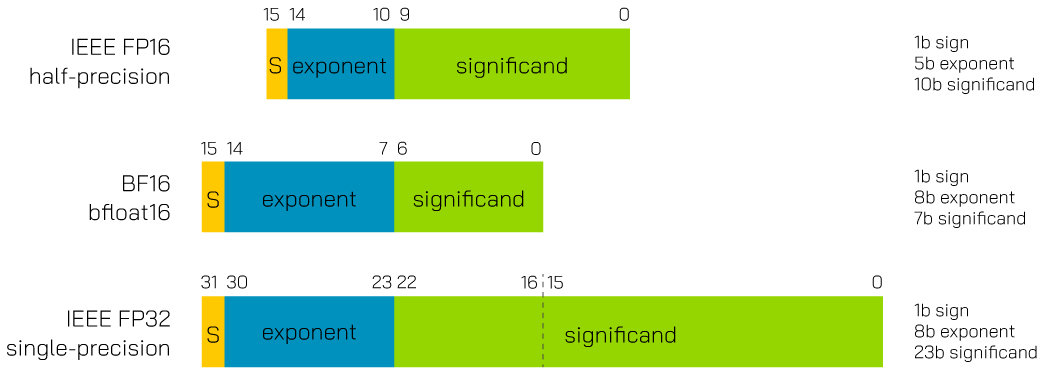
h4 ¿Qué ocurre con FP16 en modelos de IA?
En el entrenamiento con precisión mixta, los cálculos se hacen en FP16 porque son más rápidos y consumen menos memoria. Sin embargo, después de cada actualización, los resultados se validan y almacenan en FP32. Esa “copia maestra” permite corregir posibles errores de redondeo y evita que las imprecisiones se acumulen con el tiempo.
Es como hacer operaciones con calculadora de bolsillo (rápida y práctica), pero guardar siempre los resultados en un libro contable escrito con números claros y verificados. Si en algún momento la calculadora entregara un número poco preciso, el libro asegura que la base correcta nunca se pierde.
También puede pensarse como cocinar con medidas aproximadas para ir rápido, pero probando constantemente con la receta escrita original: si algo se desvía demasiado, siempre puedes volver a la referencia exacta.
BFLOAT16 (BF16) en el entrenamiento
Otro formato relevante es BFLOAT16 (BF16), desarrollado por Google. Aunque solo ocupa 16 bits, conserva el mismo rango que FP32 y sacrifica parte de la precisión en la mantisa. Esta característica lo hace menos vulnerable a desbordamientos y simplifica el proceso de entrenamiento en grandes modelos.
INT8 e INT4 en la inferencia
En la fase de inferencia, los modelos suelen transformarse a INT8 o incluso INT4 mediante técnicas de cuantización. Esta estrategia reduce de forma drástica el tamaño del modelo y acelera la velocidad de respuesta, lo que resulta crucial en dispositivos con memoria limitada.
Es comparable a comprimir música en formato MP3: ocupa mucho menos espacio y se transmite más rápido, aunque con una ligera pérdida de fidelidad. También puede pensarse como imprimir un documento a escala reducida: toda la información sigue ahí, pero en un formato más compacto y ligero de manejar.
Inferencia y cuantización en IA
Una vez entrenado un modelo pasa a la fase de inferencia, donde la prioridad ya no es aprender sino predecir con rapidez y eficiencia energética. Para lograrlo se aplica la cuantización, que convierte los pesos y activaciones —originalmente en FP32, FP16 o BF16— a formatos de menor precisión como INT8 o INT4.
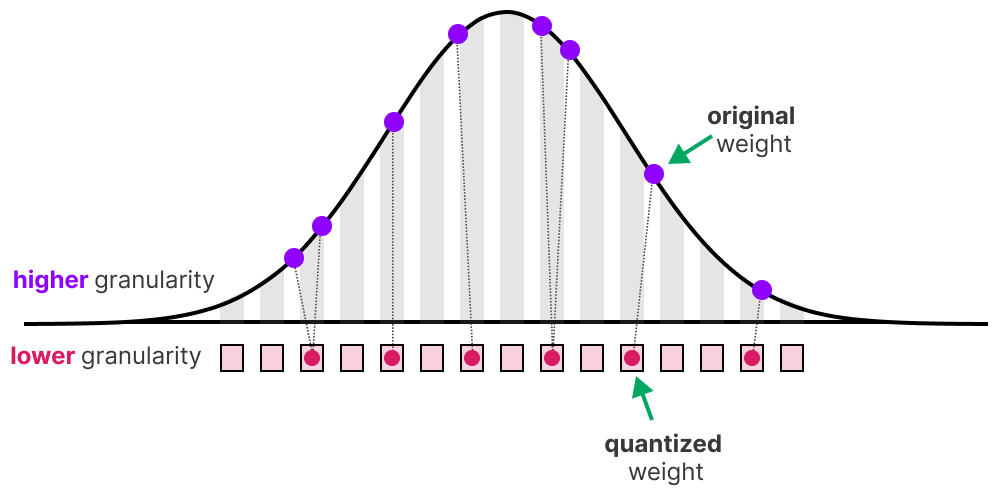
- Menor huella de memoria: un modelo en INT8 ocupa apenas una cuarta parte del espacio de su versión en FP32, lo que permite desplegarlo en teléfonos o sistemas embebidos.
- Mayor velocidad de inferencia: las GPUs y aceleradores actuales incluyen unidades de enteros mucho más rápidas y eficientes que las de punto flotante, por lo que la inferencia en INT8 puede superar varias veces a FP16.
- Latencia reducida y mejor rendimiento: al combinar menor uso de memoria y cálculos más ágiles, se obtiene una respuesta más rápida y un mayor número de predicciones por segundo, crucial en aplicaciones en tiempo real.
En términos simples, cuantizar un modelo es como comprimir música a MP3: ocupa menos espacio y se reproduce más rápido, aunque con una ligera pérdida de fidelidad. También puede compararse con imprimir un documento en formato reducido: se conserva toda la información esencial, pero en una versión más compacta y manejable.

La exigencia de máxima precisión en la supercomputación (HPC)
Mientras la IA avanza hacia formatos de baja precisión, la supercomputación sigue siendo el ámbito donde la fidelidad numérica es irrenunciable.
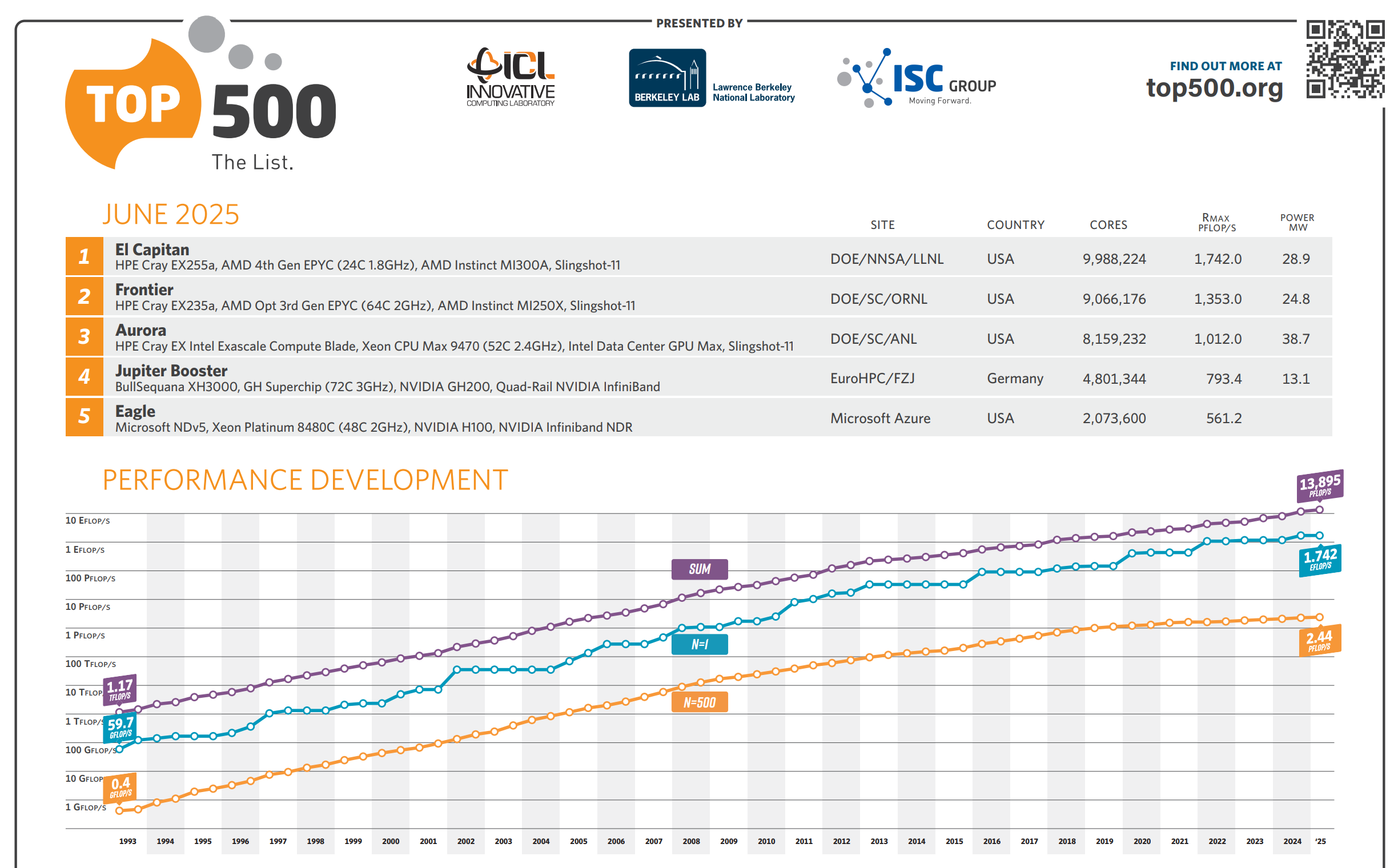
La lista TOP500, que clasifica las supercomputadoras más potentes del mundo, exige que el benchmark LINPACK se ejecute en doble precisión (FP64). Esto se debe a que las simulaciones científicas —como modelos climáticos, astrofísicos o de dinámica de fluidos— resuelven sistemas iterativos extremadamente sensibles a los errores de redondeo. Una acumulación mínima puede invalidar por completo el resultado.
La precisión de 15 a 17 dígitos decimales de FP64 es esencial para asegurar la estabilidad y confiabilidad de estas simulaciones.